L'Arbelo è una figura geometrica le cui proprietà furono studiate da Archimede; è stato uno delle prime forme geometriche il cui nome riprende un oggetto di uso quotidiano (il termine arbelo ha origini greche e indicava il "trincetto da calzolaio"1).
Per costruire un arbelo si parte da un segmento AB su cui si traccia una semi-circonferenza S1; si prende poi un punto C appartenente al segmento AB, e si costruiscono le due semi-circonferenze S2 e S3 che hanno per diametro AC e CB. L'area compresa tra le tre semi-circonferenze (e nella figura è la parte evidenziata in azzurro) è l'arbelo.

l'arbelo

Vediamo innanzitutto un paio di proprietà immediate dell'arbelo, le cui dimostrazioni — se proprio non riuscite a ricavarvele — potete trovare qui.

Ora arriviamo alla parte interessante della trattazione: chiamiamo r la retta tangente alle due circonferenze "minori" S2 e S3, che toccano queste nei punti P e Q.
Vogliamo dimostrare che il quadrilatero PCQD è un rettangolo.

Innanzitutto partiamo da una costruzione base: consideriamo solamente le circonferenze S1, S2 e S3, la retta r e i punti A, B, C, P, Q, R2 e S2.
A questi ho aggiunto le rette AP, QB, PC e CQ, oltre ai segmenti PR e QS (raggi delle circonferenze S2 e S3); ho poi chiamato F il punto di intersezione tra le rette AP e QB (in questa prima parte ho trascurato il punto D e il segmento CD).

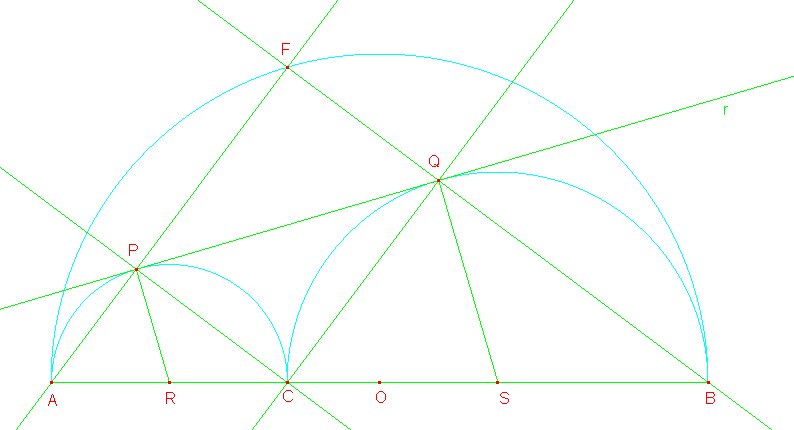
costruzione base

Scopo di questa prima parte della dimostazione è di far vedere che il quadrilatero PCQF è un rettangolo (da cui segue che il triangolo ABF è rettangolo e che dunque F si trova su S1).

Notiamo innanzi tutto che i punti A, P ed F e i punti F, Q e B sono allineati; notiamo poi che AR=PR=RC e CS=QS=SB, dunque i triangoli APR, PRC, CSQ e QSB sono isosceli.
Chiamiamo α l'angolo RAP; indichiamo subito con β il suo complementare, e con γ=π-2α e δ=π-2β.
Sappiamo che l'angolo APR=α, in quanto il triangolo APR è isoscele, dunque PRA=γ.
PRC=δ (perché il suo supplementare è γ), dunque, poiché gli angoli RPC e PCR sono uguali (perché il triangolo PRC è isoscele), abbiamo che RPC=PCR=β.
A questo punto possiamo dire che l'angolo APC è retto, in quanto somma di un angolo α (APR) e un angolo β (RPC); dunque le rette PC e AP sono perpendicolari.
Noi sappiamo poi che la retta r è tangente alle due circonferenze minori S2 e S3, dunque è perpendicolare ad entrambi i raggi PR e QS, che sono dunque paralleli. Per questo (e per le proprietà; di due rette parallele tagliate da una trasversale) l'angolo CSQ=γ.
Dunque SCQ=CQS=α; prendo ora un punto H sulla retta CQ (sotto C), e HCR=α (perché opposto di QCS).
A questo punto possiamo asserire che le rette PC e CQ sono perpendicolari anch'esse.
Effettuando per il triangolo CQB un ragionamento simile a quello del triangolo APC, notiamo che l'angolo QSB=δ, dunque gli angoli SQB=SBQ=β.
Dunque anche le rette CQ e QB sono perpendicolari; a questo punto possiamo asserire che il quadrilatero PCQF è un rettangolo.

Ora non resta da dimostrare che D ed F coincidono.
Innanzitutto disegniamo il segmento CF; gli angoli sono stato colorato per chiarezza. Basta dimostrare che il segmento CF è perpendicolare al segmento AB per finire la dimostrazione.

Sappiamo che il quadrilatero PCQF è un rettangolo, dunque i segmenti PQ e CF sono le sue diagonali, che sappiamo intersecarsi nel rispettivo punto medio, che chiameremo K. Dunque il triangolo PCK è isoscele, dunque l'angolo PCK=CPK=α; da questo segue che l'angolo ACF è retto, in quanto somma di un angolo α e di un angolo β. Dunque sia D che F sono intersezione della perpendicolare ad AB passante per C con la circonferenza S1 (dalla stessa parte), e per questo coincidono.

Altra proprietà interessante è che il rettangolo PCQD è sempre inscritto nella circonferenza S0.
Per provare ciò consideriamo i due triangoli rettangoli DPC e DQC in cui viene diviso il rettangolo dalla sua diagonale CD, che è anche il diametro della circonferenza S0.
Ogni triangolo è dunque inscritto in una semicirconferenza, ed essendo rettangolo avrà il terzo vertice sulla circonferenza S0. Dunque tutti e quattro i vertici del rettangolo appartengono alla circonferenza S0.

1personalmente non so né che cosa sia un "trincetto da calzolaio" né che forma abbia, ma presumo sia simile all'arbelo …
2R ed S sono i centri rispettivamente delle circonferenze S2 e S3